
Cette image est une ‘fractale’.
En réalité, c’est une équation mathématique mise en image.
L’histoire des fractales est particulièrement intéressante à mes yeux, car elle commence par une impossibilité. Pour faire court, voici l’histoire : tout nombre multiplié par lui même donne un nombre positif. Ainsi l’ensemble des carrés des nombres est un ensemble positif, que ces nombres soient négatifs ou pas.
De ce fait on considérait que les nombres négatifs n’avaient pas de racine carrée.
C’était absolument exclu… Impossible même !
Jusqu’au jour où un individu décida de créer un nouvel ensemble qu’il nomma les imaginaires. Un farfelu pensa t-on. Et pour ce faire, il décida que l’unité des nombres imaginaires, i, serait tel que i multiplié par lui-même, donc i au carré, serait égal à -1.
Cette invention fut en réalité très utile pour résoudre des calculs qu’on pensait impossibles. Notamment dans le domaine de l’électricité et de la physique.
Sans ces imaginaires, nous n’aurions certainement pas accès à tout ces outils magiques liés à l’électricité. On s’habitua , non sans réticence à les utiliser en tant que ‘nombres complexes’ . Et puis il y eut Benoit Mandelbrot. Ce génie mathématique utilisa les nombres complexes pour tenter de comprendre des phénomènes aléatoires dans les connexions électriques des premiers ordinateurs en réseau. Et ainsi naquirent les équations dites ‘fractales’. Dont nous apercevons la forme première dans l’image d’en haut.
Bon, et alors ?
L’histoire ne fait que commencer : cette image, apparemment fixe, n’a pas de limites.
Et voilà comment d’une impossibilité mentale est arrivé un concept qui nous fait entrer dans un univers extraordinaire où nos habitudes de raisonner de façon linéaire se voient transcendées radicalement .
Comment Benoît Mandelbrot balaye les idées reçues sur les limites des mathématiques.
Maintenant regardons comment peut s’opérer une perte du sens premier d’un concept fondamental :
L’histoire du mot : Pente
Lorsque Pythagore explique son théorème sur l’angle droit, il trace un triangle dont un côté vaut 3 unités, un autre 4 unités et le troisième, 5 unités.
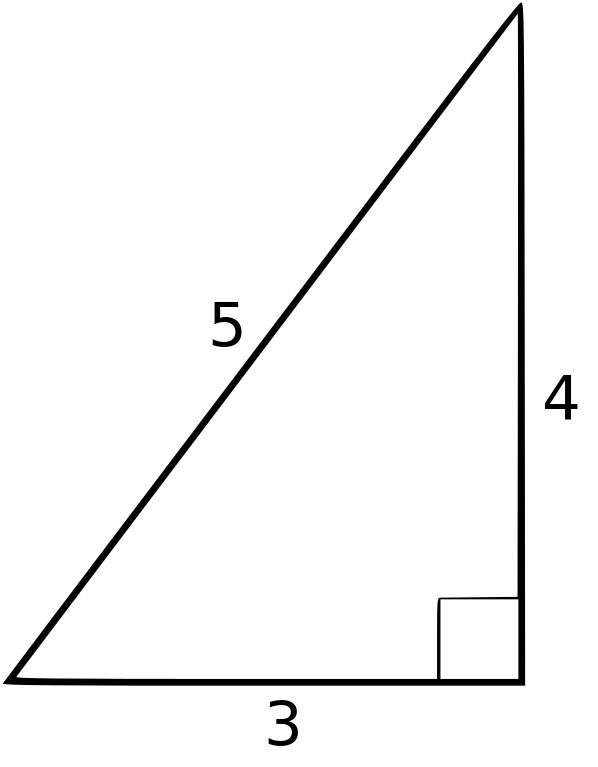
Dans cet exemple, le plus simple à vérifier et à comprendre, l’hypoténuse vaut 5. En grec, 5 se dit : Penta.
Voilà comment le mot Penta (le chiffre 5 en grec) désigne maintenant une ouverture d’angle en géométrie (la pente d’un triangle) et , dans le langage courant, la notion de descente ou de montée d’un chemin ou d’une route. Les élèves qui n’ont pas compris le raisonnement de Pythagore ont retenu l’apparence visuelle de l’hypoténuse, et non sa valeur ! Pourtant la science mathématique se veut exacte, mais je n’ai jamais rencontré de mathématicien qui reconnaisse cette grossière méprise !
